The Diagram Represents 6x2-7x 2
gruxtre
Sep 16, 2025 · 7 min read
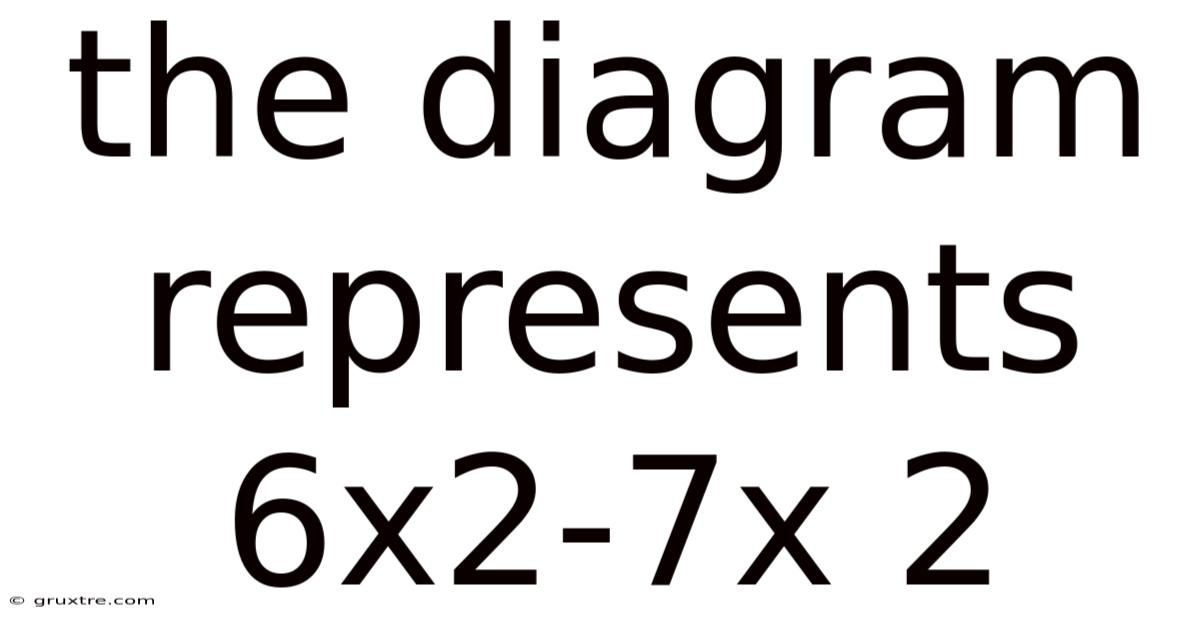
Table of Contents
Deconstructing 6x² - 7x + 2: A Deep Dive into Quadratic Expressions
This article provides a comprehensive exploration of the quadratic expression 6x² - 7x + 2, covering its factorization, graphical representation, applications, and related mathematical concepts. Understanding this seemingly simple expression unlocks a deeper understanding of algebra and its practical applications. We will move beyond simply finding the solution and delve into the why behind the methods, making this a valuable resource for students and enthusiasts alike.
Introduction: Understanding Quadratic Expressions
A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (in this case, x) is 2. They are fundamental building blocks in algebra and appear frequently in various fields, from physics (projectile motion) to economics (modeling supply and demand). The general form of a quadratic expression is ax² + bx + c, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. Our focus, 6x² - 7x + 2, perfectly fits this mold with a = 6, b = -7, and c = 2.
1. Factoring the Quadratic Expression: Finding the Roots
Factoring a quadratic expression involves rewriting it as a product of two simpler expressions. This process is crucial for solving quadratic equations (where the expression is set equal to zero) and understanding the expression's behavior. There are several methods to factor 6x² - 7x + 2, but we will explore two common approaches:
- Method 1: The AC Method
This method involves finding two numbers that multiply to the product of 'a' and 'c' (6 * 2 = 12) and add up to 'b' (-7). These numbers are -3 and -4. We then rewrite the middle term (-7x) using these numbers:
6x² - 3x - 4x + 2
Now, we can factor by grouping:
3x(2x - 1) - 2(2x - 1)
Notice that (2x - 1) is a common factor:
(2x - 1)(3x - 2)
Therefore, the factored form of 6x² - 7x + 2 is (2x - 1)(3x - 2).
- Method 2: Trial and Error
This method involves directly trying different combinations of factors of 'a' and 'c' until you find the correct combination that produces the middle term 'b'. While it might seem less systematic, it can be quicker with practice. For 6x² - 7x + 2, we consider the factors of 6 (1, 6; 2, 3) and the factors of 2 (1, 2). Through trial and error, we arrive at the same factored form: (2x - 1)(3x - 2).
2. Solving the Quadratic Equation: Finding the Zeros
Setting the quadratic expression equal to zero gives us a quadratic equation: 6x² - 7x + 2 = 0. The solutions to this equation are called the roots or zeros of the quadratic. Since we have already factored the expression, we can easily find the roots:
(2x - 1)(3x - 2) = 0
This equation is satisfied if either (2x - 1) = 0 or (3x - 2) = 0. Solving these linear equations gives us:
2x - 1 = 0 => x = 1/2 3x - 2 = 0 => x = 2/3
Therefore, the roots of the quadratic equation 6x² - 7x + 2 = 0 are x = 1/2 and x = 2/3. These values represent the x-intercepts of the parabola that represents this quadratic function.
3. Graphical Representation: Visualizing the Parabola
The expression 6x² - 7x + 2 represents a parabola when graphed on a Cartesian coordinate system. The parabola opens upwards because the coefficient of x² (a = 6) is positive. The roots we found (x = 1/2 and x = 2/3) are the x-intercepts, where the parabola crosses the x-axis. The vertex of the parabola, which represents the minimum value of the function, can be found using the formula x = -b / 2a:
x = -(-7) / (2 * 6) = 7/12
Substituting x = 7/12 back into the original expression gives the y-coordinate of the vertex. The y-intercept is found by setting x = 0, which gives y = 2.
This graphical representation provides a visual understanding of the expression's behavior, showing where the function is positive, negative, and its minimum value.
4. Applications of Quadratic Expressions:
Quadratic expressions have numerous real-world applications. Here are a few examples:
-
Physics: Projectile motion is often modeled using quadratic equations. The height of a projectile over time can be described by a quadratic function, allowing us to calculate maximum height and range.
-
Engineering: Quadratic equations are used in structural design to calculate stresses and strains in beams and other structural elements.
-
Economics: Supply and demand curves can sometimes be approximated using quadratic functions. This allows economists to model market equilibrium and price fluctuations.
-
Computer Graphics: Parabolas are used in computer graphics to create curved shapes and paths for animations and simulations.
5. Expanding Understanding: Completing the Square and the Quadratic Formula
While factoring is a useful method, it doesn't always work for all quadratic expressions. Two alternative methods for solving quadratic equations are completing the square and the quadratic formula.
-
Completing the Square: This method involves manipulating the equation to create a perfect square trinomial, which can then be factored easily. It's a powerful technique that can be used to derive the quadratic formula.
-
Quadratic Formula: This formula, x = [-b ± √(b² - 4ac)] / 2a, provides a direct solution to any quadratic equation, regardless of whether it can be factored easily. It's a fundamental tool in algebra. Applying this formula to 6x² - 7x + 2 = 0 will yield the same roots we found earlier: x = 1/2 and x = 2/3.
6. Discriminant and Nature of Roots:
The expression b² - 4ac, found within the quadratic formula, is called the discriminant. It provides information about the nature of the roots of the quadratic equation:
- b² - 4ac > 0: The equation has two distinct real roots (as in our case).
- b² - 4ac = 0: The equation has one real root (a repeated root).
- b² - 4ac < 0: The equation has no real roots; the roots are complex conjugates.
For our expression, the discriminant is (-7)² - 4(6)(2) = 49 - 48 = 1, indicating two distinct real roots.
7. Frequently Asked Questions (FAQ)
- Q: What is the difference between a quadratic expression and a quadratic equation?
A: A quadratic expression is a polynomial of degree two (e.g., 6x² - 7x + 2). A quadratic equation is a statement that sets a quadratic expression equal to zero (e.g., 6x² - 7x + 2 = 0).
- Q: Can all quadratic expressions be factored easily?
A: No. While some quadratic expressions factor neatly, others may require the quadratic formula or completing the square for solving.
- Q: What is the significance of the roots of a quadratic equation?
A: The roots represent the x-intercepts of the parabola representing the quadratic function. They also indicate the values of x that make the quadratic expression equal to zero.
- Q: What is the vertex of a parabola?
A: The vertex is the highest or lowest point on the parabola. For a parabola that opens upwards (positive coefficient of x²), it represents the minimum value of the function. For a parabola that opens downwards (negative coefficient of x²), it represents the maximum value.
- Q: How does the discriminant help in understanding the roots?
A: The discriminant determines the number and nature (real or complex) of the roots of a quadratic equation.
Conclusion: Beyond the Surface of 6x² - 7x + 2
This in-depth analysis of the seemingly simple quadratic expression 6x² - 7x + 2 reveals the rich mathematical concepts underlying it. From factoring and solving quadratic equations to visualizing the parabola and understanding its applications, we have explored a fundamental building block of algebra with significant real-world relevance. The methods discussed here—factoring, completing the square, the quadratic formula, and understanding the discriminant—are essential tools in advanced mathematics and various scientific disciplines. Mastering these concepts not only enhances algebraic skills but also provides a strong foundation for tackling more complex mathematical challenges. The seemingly simple expression 6x² - 7x + 2 serves as a powerful example of the depth and applicability of seemingly basic algebraic concepts.
Latest Posts
Latest Posts
-
Dental Instruments Names And Pictures
Sep 16, 2025
-
Adp 7 0 Board Questions
Sep 16, 2025
-
The Respiratory Membrane Consists Of
Sep 16, 2025
-
Principles Of Real Estate 1
Sep 16, 2025
-
A Coworker Didnt Clean Walmart
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about The Diagram Represents 6x2-7x 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.