Factor X 2 8x 15
gruxtre
Sep 15, 2025 · 6 min read
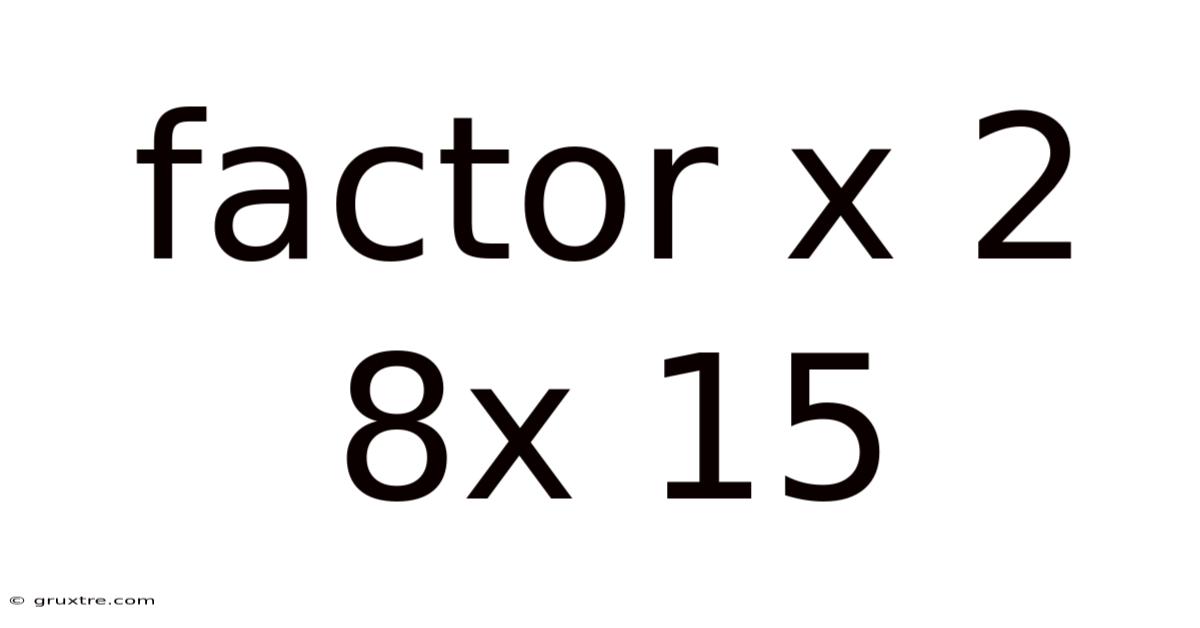
Table of Contents
Factoring the Quadratic Expression: x² + 8x + 15
This article will explore the process of factoring the quadratic expression x² + 8x + 15. We'll delve into the different methods available, explain the underlying mathematical principles, and provide practical examples to solidify your understanding. This guide is designed for students of algebra and anyone looking to refresh their knowledge of quadratic factoring. Understanding quadratic equations is fundamental in various mathematical and scientific applications.
Introduction to Quadratic Expressions
A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually x) is 2. It generally takes the form ax² + bx + c, where a, b, and c are constants. Factoring a quadratic expression involves rewriting it as a product of two simpler expressions, typically two binomials. This process is crucial for solving quadratic equations, simplifying expressions, and understanding the behavior of parabolic functions. The expression x² + 8x + 15 is a specific example of a quadratic expression where a=1, b=8, and c=15.
Method 1: Finding Factors of 'c' that Add Up to 'b'
This is the most common and often the quickest method for factoring simple quadratic expressions like x² + 8x + 15. Since the coefficient of x² (a) is 1, we can directly look for factors of the constant term (c = 15) that add up to the coefficient of x (b = 8).
Let's analyze the factors of 15:
- 1 and 15 (1 + 15 = 16)
- 3 and 5 (3 + 5 = 8)
Notice that 3 and 5 are the factors of 15 that add up to 8. Therefore, we can factor x² + 8x + 15 as follows:
(x + 3)(x + 5)
To verify this, you can expand the factored form using the FOIL method (First, Outer, Inner, Last):
- First: x * x = x²
- Outer: x * 5 = 5x
- Inner: 3 * x = 3x
- Last: 3 * 5 = 15
Combining these terms, we get x² + 5x + 3x + 15 = x² + 8x + 15, confirming our factoring is correct.
Method 2: Completing the Square
Completing the square is a more general method that works for all quadratic expressions, even those with a coefficient of x² other than 1. While it might seem more complex initially, it provides a systematic approach. Here's how it works for x² + 8x + 15:
-
Focus on the x² and x terms: Consider only x² + 8x for now.
-
Find half of the coefficient of x: Half of 8 is 4.
-
Square this value: 4² = 16
-
Add and subtract the squared value: We add and subtract 16 to maintain the equality of the expression: x² + 8x + 16 - 16 + 15
-
Factor the perfect square trinomial: The first three terms (x² + 8x + 16) form a perfect square trinomial, which factors as (x + 4)².
-
Simplify: The expression becomes (x + 4)² - 16 + 15 = (x + 4)² - 1
-
Recognize the difference of squares: (x + 4)² - 1 is a difference of squares (a² - b² = (a + b)(a - b)), where a = (x + 4) and b = 1.
-
Factor the difference of squares: This gives us [(x + 4) + 1][(x + 4) - 1] = (x + 5)(x + 3)
This method arrives at the same factored form as the previous method.
Method 3: Quadratic Formula
The quadratic formula is a powerful tool for finding the roots (solutions) of a quadratic equation. While not directly a factoring method, it can indirectly help us find the factors. The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
For x² + 8x + 15, a = 1, b = 8, and c = 15. Plugging these values into the quadratic formula gives:
x = [-8 ± √(8² - 4 * 1 * 15)] / 2 * 1 = [-8 ± √(64 - 60)] / 2 = [-8 ± √4] / 2 = [-8 ± 2] / 2
This gives us two solutions:
x₁ = (-8 + 2) / 2 = -3 x₂ = (-8 - 2) / 2 = -5
Since the roots are -3 and -5, the factored form is (x + 3)(x + 5). This method demonstrates the relationship between the roots of a quadratic equation and its factored form.
Understanding the Significance of Factoring
Factoring quadratic expressions is not just a mechanical process; it has significant implications:
-
Solving Quadratic Equations: Setting the factored expression equal to zero allows us to solve the quadratic equation. For example, (x + 3)(x + 5) = 0 implies either x + 3 = 0 (x = -3) or x + 5 = 0 (x = -5). These are the roots or solutions to the equation x² + 8x + 15 = 0.
-
Graphing Parabolas: The factored form reveals the x-intercepts of the parabola represented by the quadratic equation. The x-intercepts are the points where the parabola crosses the x-axis, which correspond to the roots of the equation (-3 and -5 in this case).
-
Simplifying Expressions: Factoring can simplify complex algebraic expressions, making them easier to manipulate and understand.
-
Applications in Science and Engineering: Quadratic equations and their solutions are fundamental in many scientific and engineering applications, such as projectile motion, optimization problems, and electrical circuits.
Advanced Applications and Extensions
The principles of factoring quadratic expressions extend to more complex scenarios:
-
Factoring Quadratics with a Leading Coefficient other than 1: Methods such as factoring by grouping or using the quadratic formula become more crucial when dealing with expressions like 2x² + 7x + 3.
-
Factoring expressions with complex roots: Some quadratic expressions have roots that are complex numbers (involving the imaginary unit i).
-
Higher-degree polynomials: The fundamental principles of factoring extend to polynomials of higher degrees, although the methods become increasingly complex.
Frequently Asked Questions (FAQ)
-
Q: What if the quadratic expression cannot be factored easily?
- A: If the expression cannot be easily factored using the methods above, the quadratic formula is the most reliable method for finding the roots and consequently deriving the factors. Some quadratic expressions may not have real roots; they will have complex roots.
-
Q: Is there only one way to factor a quadratic expression?
- A: No, there might be different ways to express the factored form, but they will ultimately be equivalent. For example, (x+3)(x+5) is the same as (x+5)(x+3). The order of the factors does not matter.
-
Q: What if the constant term (c) is negative?
- A: When 'c' is negative, you need to find factors of 'c' that have opposite signs and add up to 'b'. One factor will be positive, and the other will be negative.
-
Q: Why is factoring important in algebra?
- A: Factoring is a cornerstone of algebra, allowing simplification, solving equations, and gaining deeper insight into the behavior of polynomial functions. It's essential for further studies in calculus, linear algebra, and other advanced mathematical disciplines.
Conclusion
Factoring the quadratic expression x² + 8x + 15, whether using the method of finding factors, completing the square, or the quadratic formula, leads to the same result: (x + 3)(x + 5). Understanding these methods provides a strong foundation for tackling more complex quadratic expressions and their applications in various mathematical and real-world problems. Mastering quadratic factoring is a crucial skill for anyone pursuing studies in mathematics or related fields. The ability to efficiently factor quadratics will simplify many algebraic manipulations and enhance problem-solving capabilities. Remember to practice regularly and explore different methods to find the approach that best suits your understanding and problem-solving style.
Latest Posts
Latest Posts
-
To Cause Cancer Proto Oncogenes Require
Sep 16, 2025
-
Military Sorority Kappa Epsilon Psi
Sep 16, 2025
-
A Business Overhead Expense Policy
Sep 16, 2025
-
Electron Geometry And Molecular Geometry
Sep 16, 2025
-
What Was The Nebraska Act
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Factor X 2 8x 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.