5y 1 6x 4y 10
gruxtre
Sep 23, 2025 · 6 min read
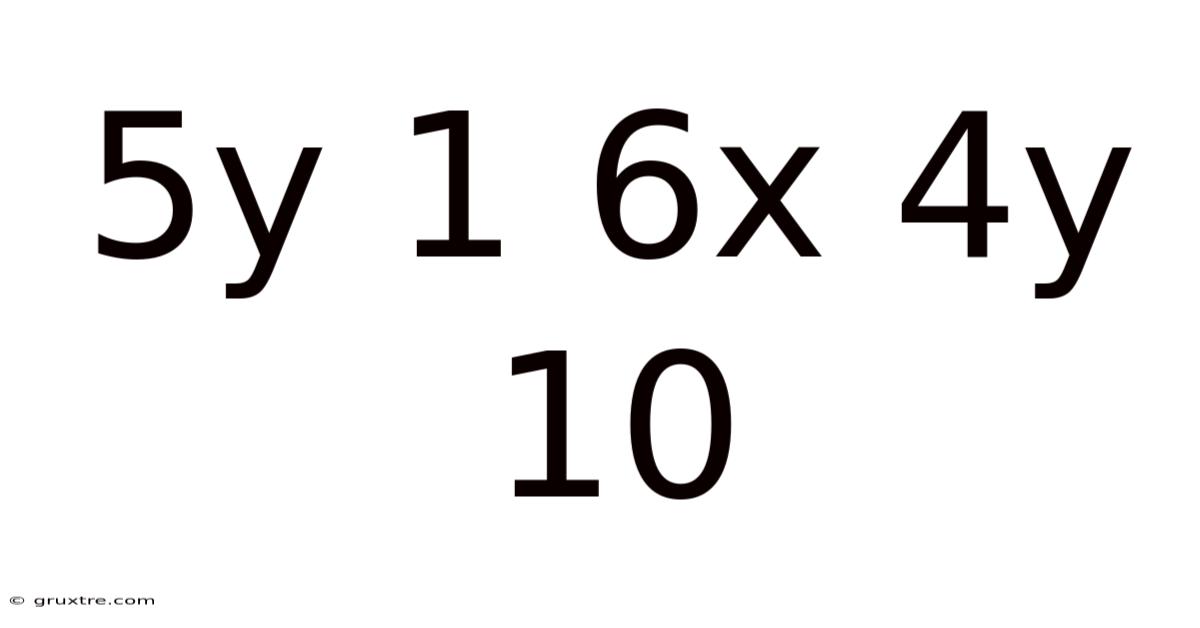
Table of Contents
Decoding the Mathematical Expression: 5y + 1 = 6x + 4y + 10
This article delves into the mathematical expression "5y + 1 = 6x + 4y + 10," exploring its solution, underlying concepts, and practical applications. Understanding this seemingly simple equation opens doors to a deeper comprehension of algebra, linear equations, and problem-solving strategies. We'll break down the solution step-by-step, discuss the significance of different approaches, and even touch upon real-world scenarios where similar equations are used.
Introduction: Understanding Linear Equations
The equation 5y + 1 = 6x + 4y + 10 is a linear equation in two variables, x and y. A linear equation is characterized by its highest power of the variables being 1. This means there are no squared terms (x², y²), cubed terms (x³, y³), or any higher powers. Graphically, a linear equation always represents a straight line. Solving this equation means finding the values of x and y that make the equation true. Since we have two variables and only one equation, we won't find a single unique solution; instead, we'll find a relationship between x and y that can be expressed in different forms.
Step-by-Step Solution: Simplifying and Rearranging
Our first step is to simplify the equation by combining like terms. Notice that both sides contain terms with y. Let's move all the y terms to one side and the x term to the other side:
-
Subtract 4y from both sides: 5y + 1 - 4y = 6x + 4y + 10 - 4y This simplifies to: y + 1 = 6x + 10
-
Subtract 1 from both sides: y + 1 - 1 = 6x + 10 - 1 This gives us: y = 6x + 9
This is our simplified solution. It expresses y in terms of x. This means for any value we choose for x, we can calculate the corresponding value of y that satisfies the original equation.
Different Representations of the Solution:
The equation y = 6x + 9 can be represented in several ways:
-
Slope-intercept form: This is the form we already have: y = mx + c, where m is the slope (6 in this case) and c is the y-intercept (9). The slope represents the rate of change of y with respect to x. A slope of 6 means that for every 1-unit increase in x, y increases by 6 units. The y-intercept is the point where the line crosses the y-axis (when x = 0).
-
Standard form: We can rearrange the equation to the standard form Ax + By = C. Subtracting 6x from both sides of y = 6x + 9 gives us -6x + y = 9. This form is useful for certain operations, particularly when dealing with systems of linear equations.
-
Graphical representation: Plotting the equation on a Cartesian coordinate system will show a straight line with a slope of 6 and a y-intercept of 9. Any point on this line represents a solution to the original equation.
Exploring Solutions with Examples:
Let's find some specific solutions by substituting different values of x:
- If x = 0: y = 6(0) + 9 = 9. So, (0, 9) is a solution.
- If x = 1: y = 6(1) + 9 = 15. So, (1, 15) is a solution.
- If x = -1: y = 6(-1) + 9 = 3. So, (-1, 3) is a solution.
- If x = 2: y = 6(2) + 9 = 21. So, (2, 21) is a solution.
The Significance of Infinite Solutions:
It's crucial to understand that a linear equation in two variables generally has infinitely many solutions. This is because there are infinitely many points on the line represented by the equation. Each point represents a pair of (x, y) values that satisfies the equation. To find a unique solution, we would need a second independent linear equation involving x and y. This would create a system of equations, allowing us to pinpoint a single intersection point.
Real-World Applications:
Linear equations like this are used extensively in various fields:
- Economics: Modeling supply and demand, calculating profit margins, and forecasting economic trends.
- Physics: Describing motion, calculating forces, and understanding relationships between physical quantities.
- Engineering: Designing structures, analyzing circuits, and modeling systems.
- Computer science: Developing algorithms, optimizing processes, and creating simulations.
For example, imagine a scenario where x represents the number of hours worked and y represents the total earnings. The equation could represent a worker's pay structure where a base pay is added to an hourly wage. Solving the equation would help determine earnings based on hours worked or vice-versa.
Further Exploration: Systems of Equations
As mentioned earlier, to find a unique solution for x and y, we need another linear equation. Let's consider a hypothetical second equation: 3x + y = 12
Now we have a system of two linear equations:
- y = 6x + 9
- 3x + y = 12
We can solve this system using various methods, such as:
-
Substitution: Substitute the expression for y from the first equation (y = 6x + 9) into the second equation: 3x + (6x + 9) = 12. Solving this equation for x will give us a unique value for x, which we can then substitute back into either equation to find the corresponding value of y.
-
Elimination: Manipulate the equations to eliminate one variable. For example, we could multiply the second equation by -1 and add it to the first equation to eliminate y.
Solving this system will yield a single solution point (x, y) that satisfies both equations.
Frequently Asked Questions (FAQ):
-
What if the equation had no solution? This would happen if the two equations represented parallel lines (they have the same slope but different y-intercepts). In this case, there would be no values of x and y that satisfy both equations simultaneously.
-
What if the equation had infinitely many solutions? This would occur if the two equations represented the same line (they are essentially multiples of each other). In this case, any point on the line would satisfy both equations.
-
Can this equation be solved graphically? Yes! Plotting both equations on the same graph will visually show the point of intersection (if a unique solution exists) or indicate parallel lines (no solution) or overlapping lines (infinite solutions).
-
Are there other methods to solve linear equations? Yes, techniques like matrix methods (Gaussian elimination, Cramer's rule) are commonly used to solve systems of linear equations, especially when dealing with a larger number of equations and variables.
Conclusion: Mastering Linear Equations
The seemingly simple equation 5y + 1 = 6x + 4y + 10 provides a rich foundation for understanding linear equations, their solutions, and their diverse applications. By mastering the process of simplifying, rearranging, and interpreting linear equations, you unlock a powerful tool for solving problems across numerous disciplines. Remember, the key is understanding the underlying concepts and choosing the most efficient method to find the solution, whether it's a single unique solution or a relationship between variables represented by a line with infinitely many points. The ability to solve and interpret linear equations is a fundamental skill that extends far beyond the classroom, opening doors to further mathematical exploration and practical problem-solving in the real world.
Latest Posts
Latest Posts
-
After A Meal Chapter 8
Sep 23, 2025
-
Heavy Amphetamine Use Drivers Ed
Sep 23, 2025
-
Free Notary Public Practice Test
Sep 23, 2025
-
John C Calhoun Apush Definition
Sep 23, 2025
-
Sample Sweet 16 Candle Speeches
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 5y 1 6x 4y 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.