4.7 5 Count By Sevens
gruxtre
Sep 10, 2025 · 5 min read
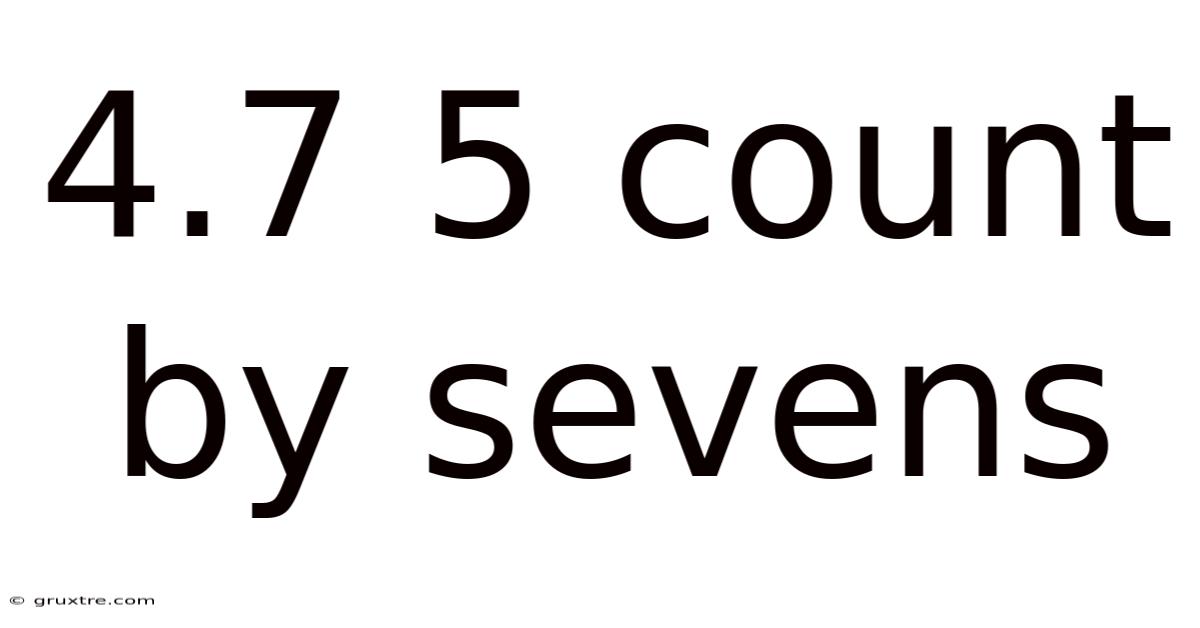
Table of Contents
Decoding the Mystery: 4.7, 5, Count by Sevens
This article delves into the intriguing mathematical puzzle presented by the seemingly disparate sequence: 4.7, 5, Count by Sevens. At first glance, it appears nonsensical. However, upon closer examination, we can uncover the underlying logic and explore the various interpretations and mathematical principles involved. This exploration will involve analyzing the number sequence, investigating potential patterns, considering different mathematical operations, and finally, offering a comprehensive understanding of the puzzle's solution. We'll also address frequently asked questions to ensure a complete and thorough explanation.
Understanding the Components: 4.7, 5, and Counting by Sevens
Before we dive into solving the puzzle, let's break down each component:
-
4.7: This is a decimal number, indicating a value between 4 and 5. Its presence suggests a potential connection to fractions or decimal operations.
-
5: This is a whole number, seemingly simple yet potentially crucial to establishing a link with the decimal 4.7.
-
Count by Sevens: This instruction signifies a sequence of numbers where each subsequent number is obtained by adding 7 to the previous one. This implies an arithmetic progression with a common difference of 7.
Exploring Potential Interpretations and Solutions
The puzzle's ambiguity allows for multiple interpretations. Let's explore some possibilities:
Interpretation 1: Rounding and Sequence Integration
One possible interpretation involves rounding 4.7 up to 5, thereby establishing a starting point for the "count by sevens" sequence. This would generate the sequence: 5, 12, 19, 26, 33, and so on. This interpretation is straightforward but might seem too simplistic given the inclusion of the decimal 4.7.
Interpretation 2: Decimal Progression with Sevens
Another approach involves considering the decimal portion (0.7) separately. We can create a sequence where we add 7 to the whole number part, and separately add 0.7 to the decimal part in a cyclical manner. This could look like:
- 4.7
- 5.4 (5 + 0, 0.7 + (-0.3))
- 12.1 (12 + 0, 0.4 + 0.7)
- 12.8 (12 + 0, 1.1 + (-0.3)) and so on. This would use modulo arithmetic where once the decimal exceeds 0.7, it resets. The whole number component follows the sevens sequence.
Interpretation 3: Weighted Average and Sequence
A more complex interpretation involves considering 4.7 and 5 as weighted averages. Suppose there is an underlying sequence X, Y, Z… where 4.7 represents a weighted average of some elements in the sequence. Similarly, 5 could also be a weighted average of different elements. This interpretation requires further information or context to be fully explored. We'd need additional data points to establish a meaningful pattern.
Interpretation 4: Hidden Mathematical Operation
The puzzle might involve a hidden mathematical operation linking 4.7 and 5. For example:
- Difference: The difference between 5 and 4.7 is 0.3. This could be a key element within a larger calculation.
- Ratio: The ratio of 5 to 4.7 is approximately 1.06. This ratio could be significant in some context. If this is a base number for the progression, we may not have enough information.
- Combination: The numbers 4.7 and 5 may be used in combination with an operation applied to this to generate an arithmetic sequence (such as using them as coefficients in a linear equation, to derive a constant rate of change to follow a progression).
The Importance of Context and Additional Information
The ambiguity of the puzzle highlights the critical role of context in mathematical problem-solving. Without additional information, multiple valid interpretations and solutions are possible. The puzzle, as presented, is underspecified. To arrive at a single, definitive answer, we require further details such as:
- The intended sequence: Are we looking for a finite or infinite sequence?
- The relationship between 4.7 and 5: How do these two numbers relate mathematically or conceptually?
- The rules governing the sequence: Are there specific restrictions or conditions beyond "count by sevens"?
Expanding the Scope: Mathematical Concepts Involved
This puzzle, despite its seemingly simple nature, touches upon several important mathematical concepts:
-
Arithmetic Progressions: The "count by sevens" instruction directly relates to arithmetic progressions, sequences where the difference between consecutive terms is constant.
-
Decimal Numbers and Fractions: The inclusion of 4.7 introduces the concepts of decimal numbers and their relationship to fractions.
-
Weighted Averages: As discussed earlier, the possibility of weighted averages adds another layer of complexity and requires a deeper understanding of statistical concepts.
-
Mathematical Modeling: Finding a solution requires constructing a mathematical model that fits the given data and satisfies the stated constraints. This involves identifying patterns, making assumptions, and testing hypotheses.
-
Modulo Arithmetic: For some interpretations, the concept of modulo arithmetic, where numbers "wrap around" after reaching a certain limit, becomes relevant, specifically related to the cyclical nature of the decimal progression.
Frequently Asked Questions (FAQ)
Q: Is there a single, definitive answer to this puzzle?
A: No, without additional information or context, there isn't a single, definitively correct answer. Multiple valid interpretations and solutions exist.
Q: How can I approach similar ambiguous mathematical puzzles?
A: Start by breaking down the components of the puzzle. Identify key terms and concepts. Explore different interpretations and try to develop mathematical models that fit the given data. Consider alternative approaches and don't be afraid to experiment. If possible, seek additional context or information.
Q: What mathematical skills are necessary to solve puzzles like this?
A: A good understanding of arithmetic, sequences and series, decimal numbers and fractions, and basic algebra is helpful. Depending on the complexity, knowledge of statistics, calculus, and other advanced mathematical concepts may be required.
Conclusion: The Power of Ambiguity and Mathematical Thinking
The "4.7, 5, Count by Sevens" puzzle serves as a valuable illustration of the power of ambiguity in mathematical problem-solving. While it may not have a single definitive answer without further clarification, its ambiguity encourages creative thinking, exploration of different approaches, and a deeper understanding of fundamental mathematical principles. The process of exploring different solutions highlights the importance of critical thinking, analytical skills, and the ability to construct and evaluate mathematical models. The seemingly simple puzzle invites us to consider the importance of context and the diverse ways in which mathematical concepts can be interconnected. Furthermore, it reveals that mathematical problems often have multiple valid solutions, highlighting the flexibility and richness of mathematical thought. The journey of exploring potential solutions, rather than finding a single definitive answer, forms the core educational benefit of this type of puzzle.
Latest Posts
Latest Posts
-
Iran Hostage Crisis Apush Definition
Sep 10, 2025
-
Answers For Fema Ics 100
Sep 10, 2025
-
Questions World Star Hip Hop
Sep 10, 2025
-
The Lymphatic Capillaries Are Quizlet
Sep 10, 2025
-
What Structure Is Highlighted Quizlet
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 4.7 5 Count By Sevens . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.